¿Qué es el máximo común divisor y cómo resolver operaciones matemáticas?
Muchos estudiantes de primaria se preguntan qué es y cómo calcular el máximo común divisor. Por eso, en las clases de matemáticas de Luca te enseñamos sobre este, uno de los temas clave del sentido numérico y el pensamiento algebraico.
¿Qué es y para qué sirve el máximo común divisor?
El máximo común divisor o MCD es útil para que los estudiantes aprendan a reconocer los denominadores comunes. Los cuales son muy útiles al momento de resolver problemas de cálculo.
En cambio, el mínimo común múltiplo es la búsqueda de la cifra más pequeña, la cual cumple la función de ser múltiplo de todos los elementos que conforman un conjunto de números.
A continuación en esta lección, los estudiantes aprenderán ejemplos de máximo común divisor que servirán para repasar y aprobar evaluaciones en clases.
¿Cómo sacar el máximo común divisor?
Para calcular el máximo común divisor es importante recordar el término divisor. Este se trata de la cifra que divide al número en partes exactas. Es decir, que el residuo no sea igual a cero o un número decimal.
Muchos estudiantes prefieren asociar al divisor como el número que está contenido de una cantidad de forma exacta, una cantidad X de veces.
En este sentido, el MCD se puede definir como la cifra más alta con la que se puede dividir un conjunto numérico para obtener un número entero como resultado.
¿Cómo sacar el máximo común divisor?
Para encontrar el MCD se pueden aplicar dos métodos, principalmente.
1. Identifica el MCD de cada número
Este el primero de los métodos y es también el más sencillo. Aunque también puede ser el más demorado. Para llevarlo a cabo deberás:
- Escribir todos los divisores de cada número e identificar los divisores comunes.
- El número mayor entre ellos será el MCD.
Un ejemplo para entender este método es descubrir cuál es el MCD entre 15 y 25.
Cómo calcular el MCD de 15:
15/1 = 15 (Entonces 1 y 15 son números divisores de 15)
15/2 = 7 con el resto de 1 (Entonces 2 no es un número divisor de 15)
15/3 = 5 (Entonces 3 y 5 son números divisores de 15)
15/4 = 3 con el resto de 3 (Entonces 4 no es un número divisor de 15)
Cómo calcular el MCD de 25:
25/1= 25 (Entonces 1 y 25 son números divisores de 25)
25/2 = 12 con el resto de 1 (Entonces 2 no es un número divisor de 25)
25/5 = 5 (Entonces 5 es número divisor de 25)
De esta manera, el máximo común divisor entre estos dos números es 5.
Descomposición en factores primos
Para poner en práctica este método deberás:
- Descomponer cada uno de los números en factores primos.
- Identificar y señalar los factores comunes.
- Señalar entre los factores comunes, aquel con menor exponente.
- Multiplicar los factores elegidos.
Para ejemplificar este método buscaremos el MCD de 20 y 15.
- Factores primos
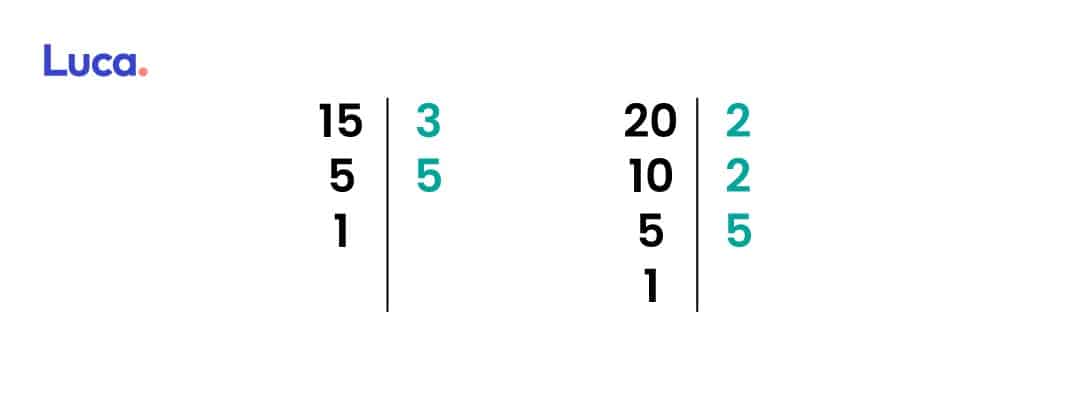
2. Números como producto de sus factores primos.
Factores primos de 15: 3X5.
Factores primos de 20: 2^2 X 5.
3. Identifica el factor primo común con menor exponente.
Factor común con mínimo exponente: 5.
4. MCD de 15 y 20 es 5.
Ya tienes algunos ejemplos y los conocimientos clave para entender al máximo común divisor. Con cada nuevo ejercicio que desarrolles se te hará mucho más fácil. Además, contarás con la ayuda de Luca en el aula. Somos la plataforma educativa con las mejores metodologías y recursos y, pronto, seremos tus mejores compañeros de estudio.




Qué bueno el texto, me ha servido para entender el máximo común divisor.
Recomiendo estos textos de ayuda escolar y educativo y los aliento a que contiúen creando este tipo de material que contribuyen a la formación de todos.
Muchas gracias, Rafael. Esperamos que nos sigas acompañando y recomendando en publicaciones futuras.